里兹法求解薄板振动方程

我的研究方向是对微机电压电水听器进行建模，查阅相关文献时往往会遇到这个偏微分方程：

$D\nabla^{4}w+\rho_{h}w_{tt}=0$

先不管参数 $D,\rho_{h}$，让我们关注方程本身，把这个式子当作单纯的“计算对象”。我没能在 Wolfram 的帮助文档里找到“一键式”的数值求解方法，而解析解只能处理固定边圆板、简支边圆板和简支边方板等特殊情况，如果是蜂巢形的水听器单元呢？

面对偏微分方程难解的问题，里兹法的思路大概是：先通过能量分析，把方程问题变成优化问题，再用基函数逼近真实解。在基函数设置时，就可以考虑薄板形状和边界条件的问题，从而得到一个比较通用的程序，利用 Wolfram 语言的内置函数，还可以把这个程序写得更简单。

最小作用量，最小物理知识

于我而言，“最小作用量”这套方法是在最小化物理知识的基础上，解决所面临的建模问题。

首先，还是要计算出薄板的动能和势能表达式：

$\begin{align} T&=\frac{\omega^{2}}{2}\rho_{h}a^{2}\iint_{\bar A}\bar w^{2}(x,y)\mathrm{d}x\mathrm{d}y\\ U&=\frac{1}{2}Da^{-2}\iint_{\bar A}(\nabla^{2}\bar w)^{2}\mathrm{d}x\mathrm{d}y \end{align}$

其中 $T$ 就是众所周知的 $m v^2/2$ 这个形式，$U$ 则需要参考基尔霍夫薄板理论的应力、应变表达式，并代入线弹性材料应变能的公式里。

补充两点：

积分区域经过尺度变换，所以可以将尺度系数 $a$（不妨理解为“半径”）提到积分之外。
为了简化过程，选取了 $U$ 的最简形式，这仅对固定边界条件成立，如果是更一般的情况，应该添加一项：

$-2(1-\nu)\left[\frac{\partial^{2} w}{\partial x^{2}} \ \frac{\partial^{2} w}{\partial y^{2}}-\left(\frac{\partial^{2} \ w}{\partial x \partial y}\right)^{2}\right]$

然后，用二者之差代表最小作用量：

$\Pi=T-U$

“最小”并不意味着“最小”，只是取得极值，或者说对于自变函数 $w(x,y)$ 来说，变分 $\delta\Pi=0$。所以，虽然里兹采用的能量泛函为 $U-T$，但这一点区别无关紧要。

另外，最小作用量的被积函数部分，就是拉格朗日量（或拉格朗日密度）。将其代入欧拉-拉格朗日方程后，同样可以得到前面给出的偏微分方程。对我来说，这要比从微元体出发的推导容易太多。

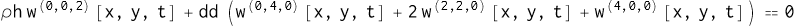
1 2	Needs["VariationalMethods`"] EulerEquations[1/2 \[Rho]h D[w[x, y, t], t]^2 - 1/2 dd (Laplacian[w[x, y, t], {x, y}])^2, w[x, y, t], {x, y, t}] // FullSimplify

用什么基函数来逼近真实解？

很多文章选取的基函数都很巧妙，既要满足边界条件，又要起到逼近真实解的作用。但我们打算得到比较通用的程序，就不能把基函数形式限制在一种特殊场景中。

所以，不妨将基函数写作两项相乘的形式¹：

边界方程

灰色部分为薄板区域，红色部分为薄板边界：

1	Graphics[{LightGray, #, Red, RegionBoundary@# }] & /@ {Disk[], Rectangle[{-1, -1}, {1, 1}], RegularPolygon[6]} // GraphicsRow

对于圆形薄板来说，其边界方程为：

$(x^2+y^2-1)^{i}$

对于方形薄板来说，其边界方程为：

$(x-1)^{i}(x+1)^{j}(y-1)^{k}(y+1)^{l}$

注意式子里的上标代表该边界的边界条件，$0$ 对应于自由边界条件，$1$ 对应于简支边界条件，$2$ 对应于固定边界条件。

如果是正六边形板，这个边界方程就很难直接写出。可以先写一个函数，能输入各顶点坐标，输出边界方程：

(* 计算两点之间的线方程 *)
lineEquation[{p1_, p2_}, {x_, y_}] := 
  (x - p2[[1]]) (p1[[2]] - p2[[2]]) - (y - p2[[2]]) (p1[[1]] - p2[[1]])

(* 将点列表转换为成对的点 *)
pointsPair[points_List] := 
  Partition[Riffle[#, RotateLeft[#]], 2] & @ points

(* 计算多边形的边界 *)
polygonBorder[points_List, {x_, y_}] := 
  Times @@ (lineEquation[#, {x, y}] & /@ pointsPair @ points)

正六边形的六个顶点即为：

1	CirclePoints[6]

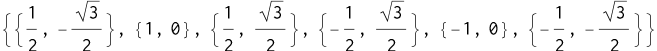
可计算得到边界方程：

1	polygonBorder[%, {x, y}]

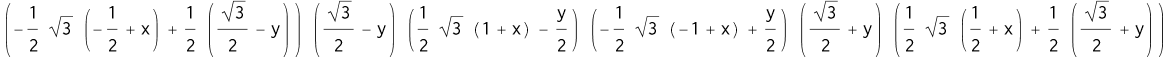
逼近函数

使用勒让德多项式逼近函数：

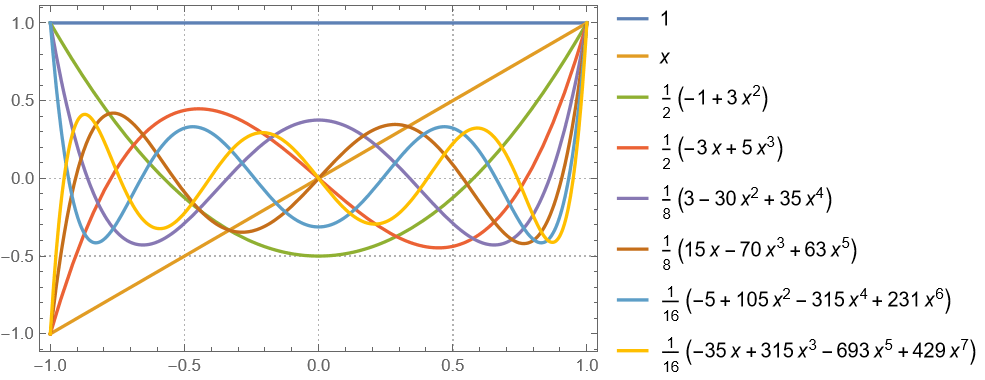
多项式两两相乘，得到用于函数逼近的二元基函数：

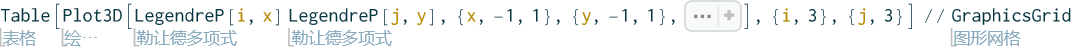
以固定边界圆板为算例，其基函数形式为：

1	basicFunctions = Table[LegendreP[i - 1, x] LegendreP[j - 1, y], {i, 4}, {j, 4}] (x^2 + y^2 - 1)^2 // Flatten

终于变成矩阵问题

为方便计算，先把近似解写成基函数加权求和的形式：

$\hat w(x,y)=\sum\limits_{k=1}^{K}c_ {k}\psi_{k}(x,y)$

代入动能 $T$、势能 $U$ 的表达式中，积分部分即为系数矩阵的“二次型”：$\boldsymbol{c}^\mathrm{T}\boldsymbol{Mc}$ 和 $\boldsymbol{c}^\mathrm{T}\boldsymbol{Kc}$，其中 $\boldsymbol{M},\boldsymbol{K}$ 分别称为质量矩阵和刚度矩阵，矩阵元素的表达式为²：

$\begin{align} k_{ij}&=\iint_{\bar A}\nabla^{2}\psi_{i}\cdot\nabla^{2}\psi_{j} \ \mathrm{d}x\mathrm{d}y\\ m_{ij}&=\iint_{\bar A}\psi_{i}\cdot\psi_{j}\mathrm{d}x\mathrm{d}y \end{align}$

继续前面的例子：Wolfram 语言允许我们在区域上进行积分，可计算出刚度矩阵和质量矩阵：

1
2

kmatrix = Table[Integrate[Laplacian[basicFunctions[[i]], {x, y}] Laplacian[basicFunctions[[j]], {x, y}], Element[{x, y}, Disk[]]], {i, 1, 16}, {j, 1, 16}];
mmatrix = Table[Integrate[basicFunctions[[i]] basicFunctions[[j]], Element[{x, y}, Disk[]]], {i, 1, 16}, {j, 1, 16}];

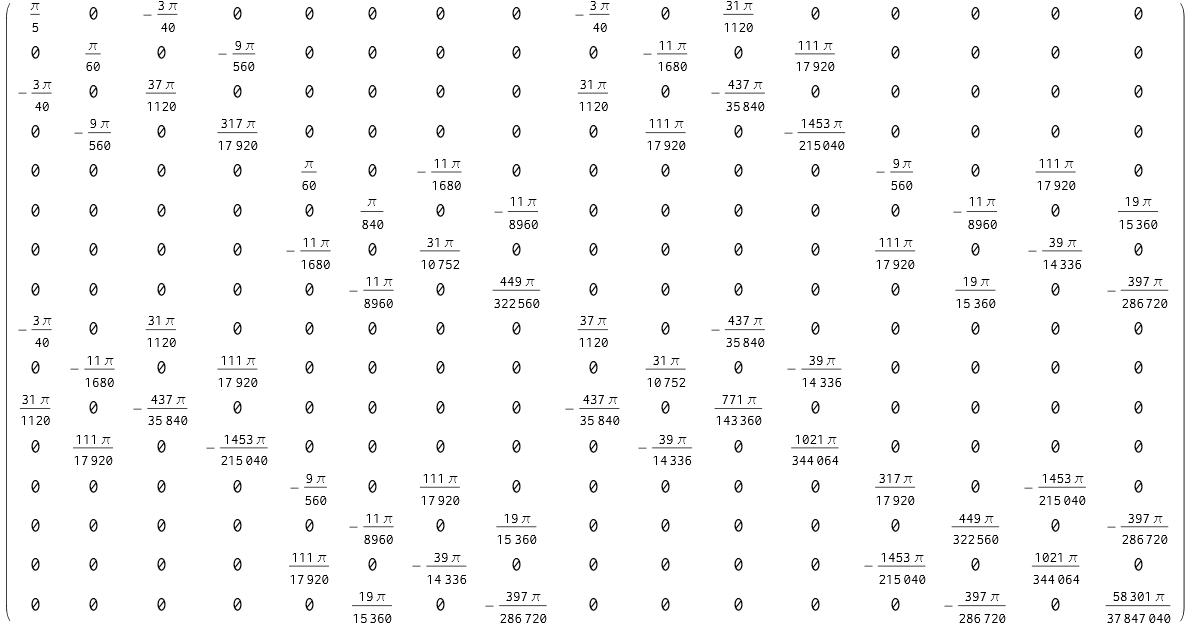
甚至可以发现，对于圆板来说，两个矩阵的所有元素竟然都有精确解：

1	kmatrix // MatrixForm

1	mmatrix // MatrixForm

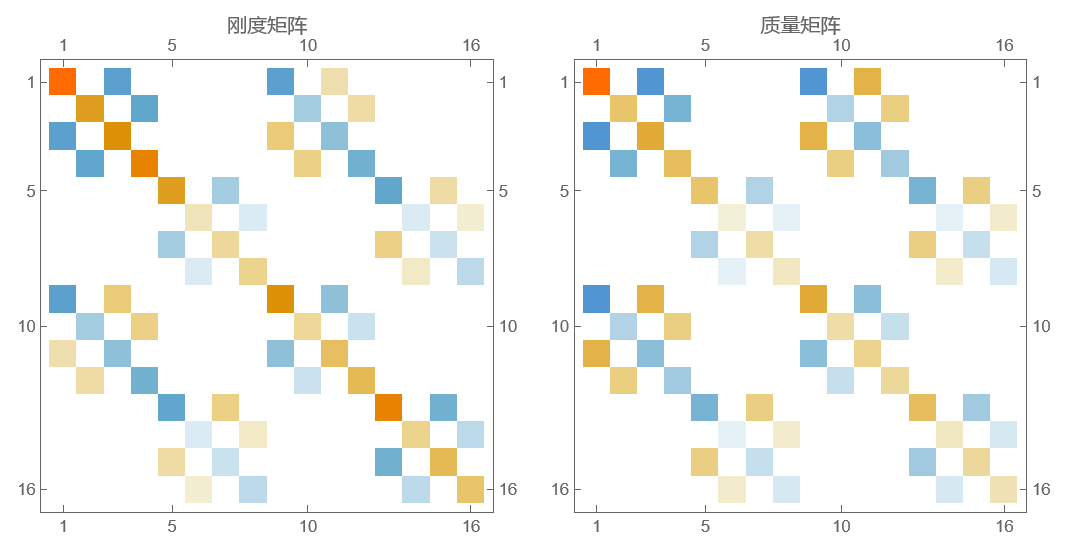
用矩阵热图进行可视化，不难发现这两个矩阵都是对称矩阵，利用这一特性可以减少运算量。

1	MatrixPlot[#[[1]], PlotLabel -> #[[2]]] & /@ {{kmatrix, "刚度矩阵"}, {mmatrix, "质量矩阵"}} // GraphicsRow

通过选取合适的系数，取得作用量的极值，即作用量对向量 $\boldsymbol{c}$ 求导为零：

$\frac{\partial\Pi}{\partial c}=0$

化简得到：

$(\boldsymbol{K}-\lambda^{4}\boldsymbol{M})\boldsymbol{c}=0$

1	{vals, coefs} = Eigensystem[{N@kmatrix, N@mmatrix}, -4];

把优化问题转化为质量矩阵和刚度矩阵的广义特征值求解问题，将特征向量 $\boldsymbol{c}$ 与基函数向量 $\boldsymbol{\psi}$ 点乘，即得近似解表达式。可将前四个模态的密度图绘制如下：

其中的密度图为模态振型，上面的数字为特征值 $\lambda$，与以下微分特征方程中的特征值 $k$ 与半径 $a$ 的乘积近似相等：

$\nabla^{4}w(r)=k^{4}w(r)$

程序简化并总结为函数

参考上述分析过程，有以下几点优化空间：

第一，质量矩阵、刚度矩阵均为对称矩阵，可削减计算量：

1
2
3

Table[N@Integrate[Laplacian[basicFunctions[[i]], {x, y}] Laplacian[basicFunctions[[j]], {x, y}], Element[{x, y}, Disk[]]], {i, 1, 16}, {j, 1, 16}]; // RepeatedTiming

(*{1.52804, Null}*)

1
2
3

Table[N@Integrate[Laplacian[basicFunctions[[i]], {x, y}] Laplacian[basicFunctions[[j]], {x, y}], Element[{x, y}, Disk[]]], {i, 1, 16}, {j, 1, i}]; // RepeatedTiming

(*{0.813599, Null}*)

第二，计算积分时可并行计算，以减少程序耗时：

1
2
3

$ProcessorCount

(*4*)

1
2
3

ParallelTable[N@Integrate[Laplacian[basicFunctions[[i]], {x, y}] Laplacian[basicFunctions[[j]], {x, y}], Element[{x, y}, Disk[]]], {i, 1, 16}, {j, 1, i}]; // RepeatedTiming

(*{0.355318, Null}*)

第三，为编写更具一般性的程序，应使用数值积分。对于矩阵中存在的大量零元素，需要设定合适的准确度目标：

1
2
3

ParallelTable[NIntegrate[Laplacian[basicFunctions[[i]], {x, y}] Laplacian[basicFunctions[[j]], {x, y}], Element[{x, y}, Disk[]], AccuracyGoal -> 5], {i, 1, 16}, {j, 1, i}]; // RepeatedTiming

(*{1.47974, Null}*)

于是，将优化后的函数整合为一个程序包：

Clear[polygonBorder, lineEquation, pointsPair]

Get[FileNameJoin[{NotebookDirectory[], "RitzMethod.wl"}]]

?RitzSolver

对于上面的固定边界圆板，可以这样调用函数：

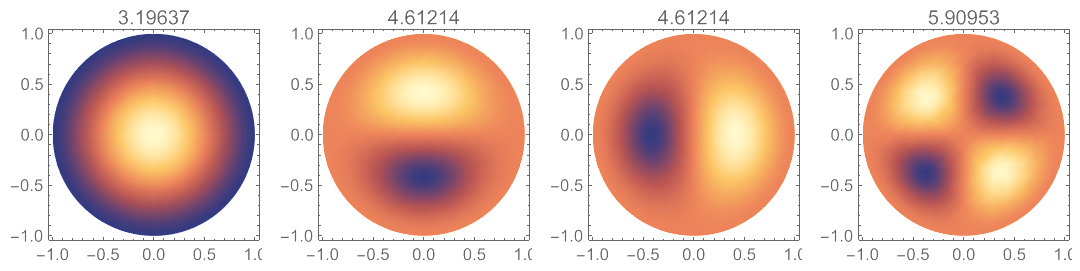
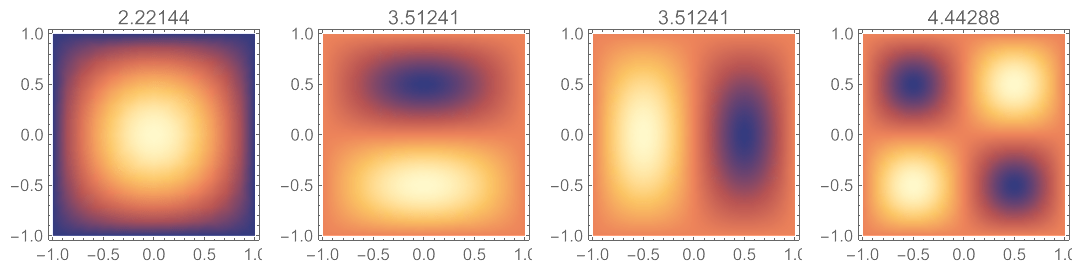
对于简支边界方板，需要多设置两个参数，一个是边界方程的指数，另一个是泊松比：

实际上，参考此算例的解析解表达式，可知泊松比并不影响结果：

1	SSSquare[{m_, n_}, {x_, y_}] := {Pi Sqrt[(m/2)^2 + (n/2)^2], Sin[Pi m (x + 1)/2] Sin[Pi n (y + 1)/2]}

绘图，并与里兹解作比较：

1	DensityPlot[#[[2]], {x, -1, 1}, {y, -1, 1}, PlotLabel -> N@#[[1]]] & /@Flatten[#, 1] &@Table[SSSquare[{i, j}, {x, y}], {i, 2}, {j, 2}] // GraphicsRow

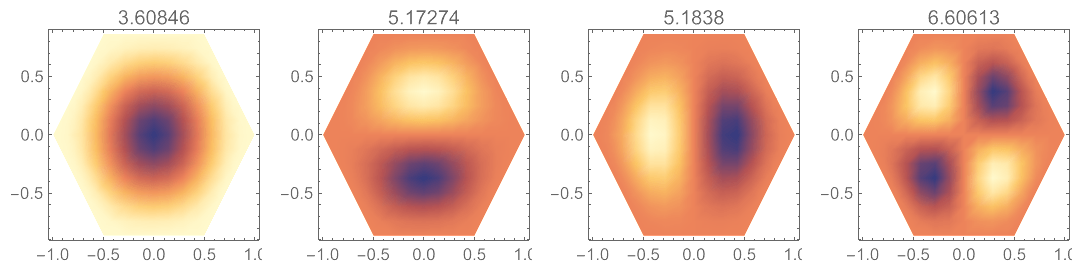
最后是固定边界正六边形板，也就是我在文章最开始讲的“蜂巢形的水听器单元”：

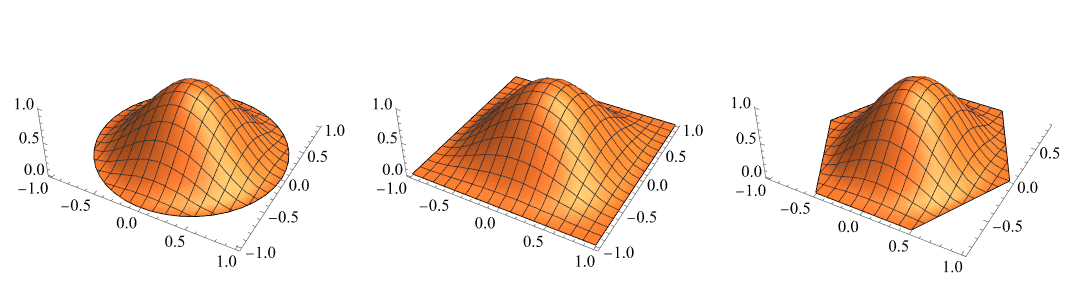
第一个解看上去有些奇怪，可以绘制出立体图形，只是凹陷而已：

本文处理的方程是齐次的，所以不管解的幅值是多少，都能满足该方程，但为了方便后续处理，一般会对幅值作归一化：

为了降低理解难度，文中略去了许多细节。比如一般边界条件的刚度矩阵元素表达式，你可以在程序文件中找到。至于更详细的推导过程，可以参考下面列出的两篇文献，或者自行搜索“基尔霍夫薄板理论”的相关内容。

24/12/04

¹. Zhao, J. (2023). Variable stiffness discrete Ritz method for free vibration analysis of plates in arbitrary geometries. Journal of Sound and Vibration, 553, 117662. ↩

². Leissa, A. W. (2005). The historical bases of the Rayleigh and Ritz methods. Journal of Sound and Vibration, 287(4–5), 961–978. ↩

Joffoo's blog