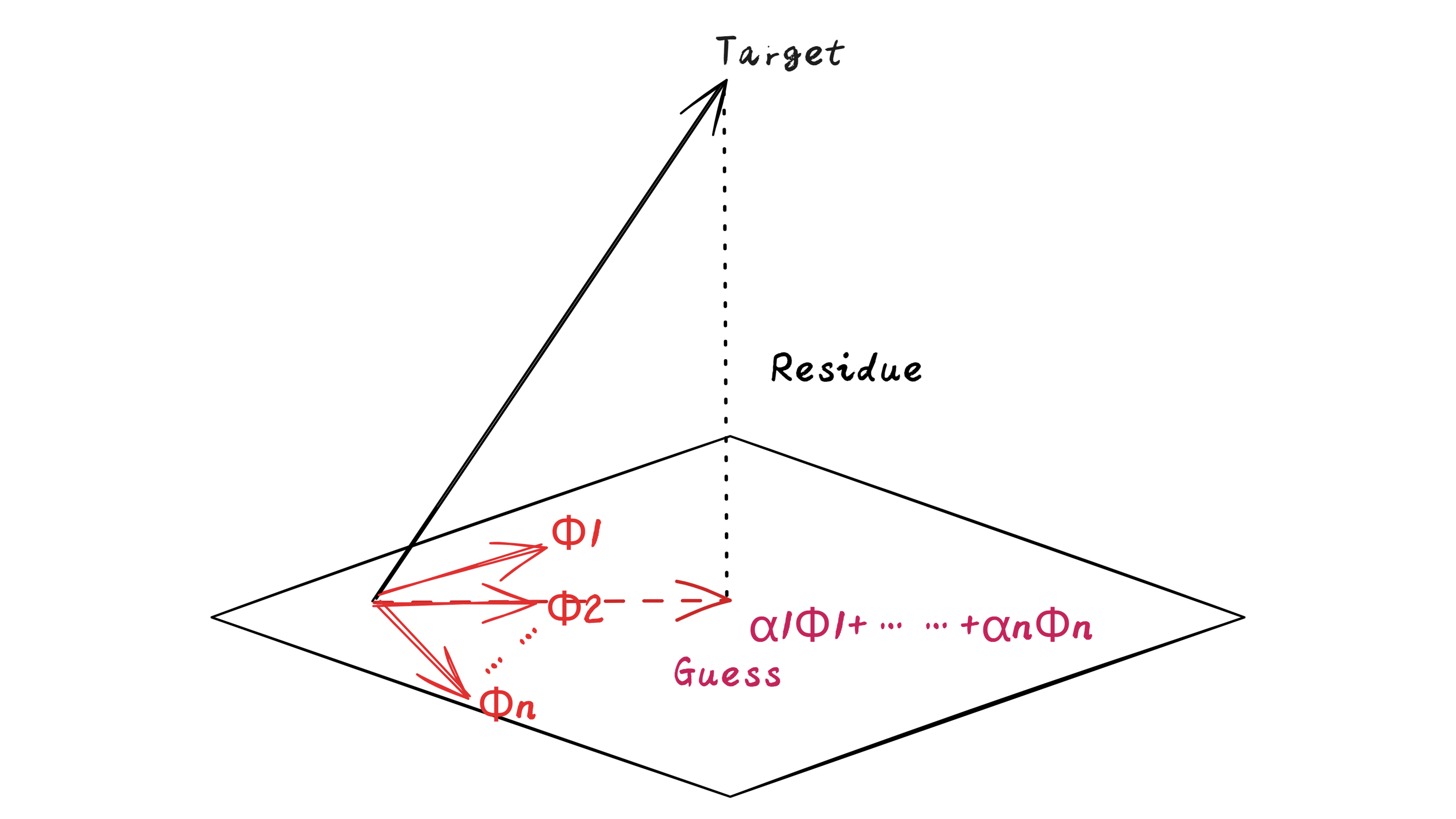
这是我用白板软件 Excalidraw 绘制的，这幅图在我粗疏的学习过程中反复得见。第一次见可能是格拉姆-施密特正交化（Gram-Schmidt orthogonalization），图中的箭头都是正常的向量。第二次见可能是维纳滤波器（Wiener filter），细节已经忘光了，图中的箭头好像是随机过程。第三次见就是伽辽金法（Galerkin method）了，图中的箭头现在是函数。
还是处理这个方程
\[ D\nabla^{4}w+\rho_{h}w_{tt}=0 \]
上一篇文章里提到“最小物理知识”，其实相比里兹法的能量泛函，伽辽金法涉及的物理知识还要更少一些。
先分离变量，把上面的方程变得只与空间中的变量 \(x,y\) 有关：
\[ \nabla^{4}w-k^{4}w=0 \]
和里兹法一样，把近似解写成基函数加权求和的形式：
\[ \hat w(x,y)=\sum_{j}c_ {j}\psi_{j}(x,y) \]
回想文章的题图，伽辽金法找近似解思路是：当近似解 \(\hat w\) 最接近真实解 \(w\) 时，每个基函数 \(\psi_{i}\) 与根据方程得到的残差 \(\nabla^{4}\hat w-k^{4}\hat w\) 正交。
先定义一个内积形式：函数相乘后在板区域内积分
\[ \langle f,g\rangle=\iint_{A}f(x,y)g(x,y)\mathrm{d}x\mathrm{d}y \]
逼近目标可以写作：
\[ \iint_{A}\psi_{j}(\nabla^{4}\hat w-k^{4}\hat w)\mathrm{d}x\mathrm{d}y=0 \]
可以展开为下式：
\[ \sum\limits_{j}c_{j}\iint_{A}\psi_{i}\nabla^{4}\psi_{j}\mathrm{d}x\mathrm{d}y-k^{4}\sum\limits_{j}c_{j}\iint_{A}\psi_{i}\psi_{j}\mathrm{d}x\mathrm{d}y=0 \]
为了获得与里兹法一致的结果，对这两个积分作尺度变换，得到：
\[ \sum\limits_{j}c_{j}\iint_{\bar A}\psi_{i}\nabla^{4}\psi_{j}\mathrm{d}x\mathrm{d}y-k^{4}a^{4}\sum\limits_{j}c_{j}\iint_{\bar A}\psi_{i}\psi_{j}\mathrm{d}x\mathrm{d}y=0 \]
至此，可以把上式写成矩阵特征值问题：
\[ (\boldsymbol{K}-\lambda^{4}\boldsymbol{M})\boldsymbol{c}=\boldsymbol{0} \]
其中，质量矩阵 \(\boldsymbol{M}\) 和刚度矩阵 \(\boldsymbol{K}\) 的元素表达式分别为
\[ \begin{align*} m_{ij}&=\iint_{\bar A}\psi_{i}\psi_{j}\mathrm{d}x\mathrm{d}y\\ k_{ij}&=\iint_{\bar A}\psi_{i}\nabla^{4}\psi_{j}\mathrm{d}x\mathrm{d}y \end{align*} \]
自伴随算子
相比能量泛函得到的 \(k_{ij}\)（固定边界条件），这次得到的式子看似有些不同。
\[ k_{ij}=\iint_{\bar A}\nabla^{2}\psi_{i}\cdot\nabla^{2}\psi_{j} \ \mathrm{d}x\mathrm{d}y \]
为了找到关联，先要补充一个条件。利用上面定义的内积形式，根据格林第二定理：
\[ \langle\nabla^{2} f,g\rangle=\langle f,\nabla^{2} g\rangle+\oint_{\partial A} \left(g(x,y) \frac{\partial f(x,y)}{\partial\boldsymbol{n}}- f(x,y)\frac{\partial g(x,y)}{\partial\boldsymbol{n}}\right)\mathrm{d}s \]
\(\partial A\) 为板区域 \(A\) 的边界，如果 \(f,g\) 是满足固定边界条件或简支边界条件的模态振型函数，那么在边界上就有 \(f=g\equiv0\)，于是上式就可以大幅化简为
\[ \langle\nabla^{2} f,g\rangle=\langle f,\nabla^{2} g\rangle \]
对于这个情况，称拉普拉斯算子 \(\nabla^{2}\) 为自伴随算子。按照上面的规则，可以找到两种 \(k_{ij}\) 之间的关系：
\[ k_{ij}=\langle\psi_{i},\nabla^{2}\nabla^{2}\psi_{j}\rangle=\langle\nabla^{2}\psi_{i},\nabla^{2}\psi_{j}\rangle \]
或许存在“悖论”
总结一下：对于固定边界条件，里兹法和伽辽金的结果都是 \(k_{ij}=\langle\nabla^{2}\psi_{i},\nabla^{2}\psi_{j}\rangle\)。但对于简支边界条件，里兹法给出的 \(k_{ij}\) 显然更为复杂（复杂到上篇文章里都没有直接写出来）：
\[ \begin{align} k_{ij}&=\iint_{\bar A}\left[\nabla^{2}\psi_{i}\nabla^{2}\psi_{j}\right.\\&\quad\left.-(1-\nu)\left(\frac{\partial^{2}\psi_{i}}{\partial x^{2}}\frac{\partial^{2}\psi_{j}}{\partial y^{2}}+\frac{\partial^{2}\psi_{j}}{\partial x^{2}}\frac{\partial^{2}\psi_{i}}{\partial y^{2}}\right)\right.\\&\left.\quad+2(1-\nu)\frac{\partial^{2}\psi_{i}}{\partial x\partial y}\frac{\partial^{2}\psi_{j}}{\partial x\partial y}\right]\mathrm{d}x\mathrm{d}y \end{align} \]
式中 \(\nu\) 为泊松比，伽辽金法的推导过程全然没有涉及。
用 RitzSolver
试算一下（与上篇文章相比，对程序包作了一点不重要的改动），可见简支方板和正六边形板的第一特征值
\(\lambda_{1}\)
随泊松比的变化保持恒定（形状看 PlotMarkers），而简支圆板的
\(\lambda_{1}\)
随泊松比的增大而单调递增。
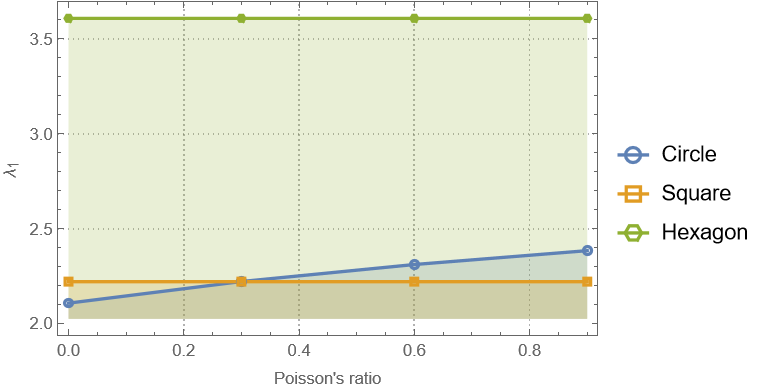
简支边界的圆板与泊松比有关，而多边形板与泊松比无关。考古之后发现这一现象被称为“polygon-circle paradox”，也就是说，你可能会预期随着多边形的边数不断增加，趋近于圆形时，多边形板的解会与圆形板的解趋于一致，但实际上并非如此。
画一下取泊松比 \(\nu=1\) 时简支边界的多边形薄板模态振型，分别是六边形、十边形、十五边形和二十边形：
可以看出随着多边形边数的增加，边界的“约束”也越来越大。对比 \(\nu=1\) 时的简支边界圆板和固定边界圆板，可见简支边界二十边形薄板的“约束”甚至大于固定边界的圆板：
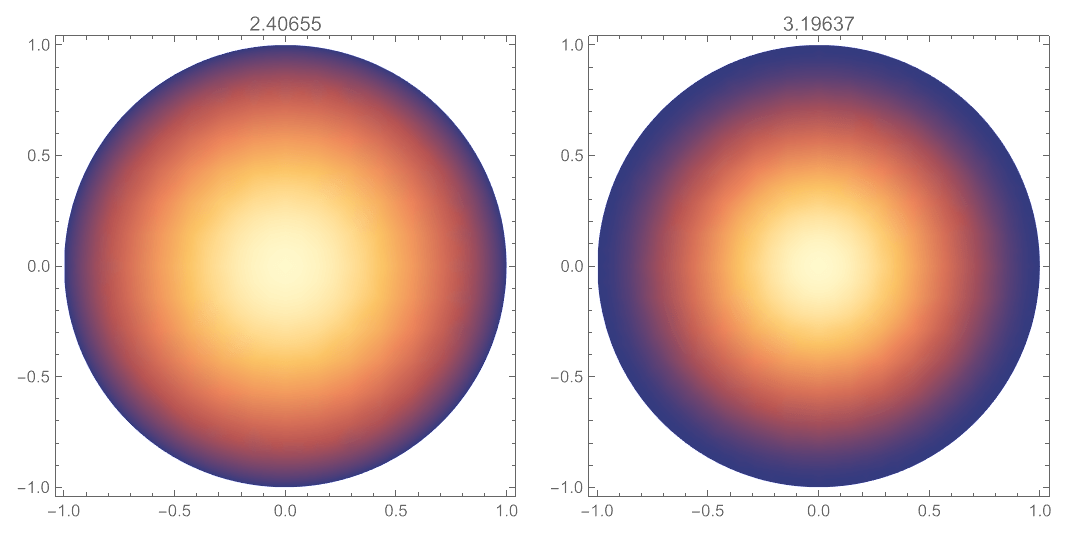
这个悖论的关键好像在于边界的曲直，但我没有真正看穿它。实际上我连“简支边界条件”都不是特别理解。这篇文章只是把我算出来的和查到的东西总结起来，然后放在这里。
24/12/27
