零基础「千里江山图」入门

在天津美院的美术馆看到一个学生作品，大概是受到了《千里江山图》的启发（如图所示，图片经过 FLUX Kontext 模型后期处理）。我突发奇想，感觉这是 Wolfram 语言的 Plot3D 可以画出来的东西，所以回到家就立马试上一试。

取色

我先截取了《千里江山图》的一个局部：

从网上搜一下 Wolfram 语言中“颜色”的相关操作，看到一个资源函数 ImageColorFunction，可以方便地得到同款配色：

jiangshanColor = ResourceFunction["ImageColorFunction"][img]

RegionPlot[True, {x, 0, 1}, {y, 0, 1}, 
 ColorFunction -> jiangshanColor, Frame -> False, 
 Axes -> {True, False}, AspectRatio -> .1, ImageSize -> 500]

这里需要注意一下：该函数默认给出的配色，是数值大处为土黄，在后续绘制时需要补充一个 1-z 的翻折操作。

山形

对于山形的构造，Gemini 的第一反应是，利用高斯函数叠加来模拟：

1
2
3

mainPeak[x_, y_] := 2 * Exp[-((x - 0.5)^2 + (y - 0.5)^2) / 0.1] +
1.5 * Exp[-((x + 0.5)^2 + (y + 0.2)^2) / 0.2] +
1.8 * Exp[-((x - 0.1)^2 + (y + 0.6)^2) / 0.15]

用一下上面的配色看看效果：

1
2
3

Plot3D[mainPeak[x, y], {x, -1.5, 1.5}, {y, -1.5, 1.5}, 
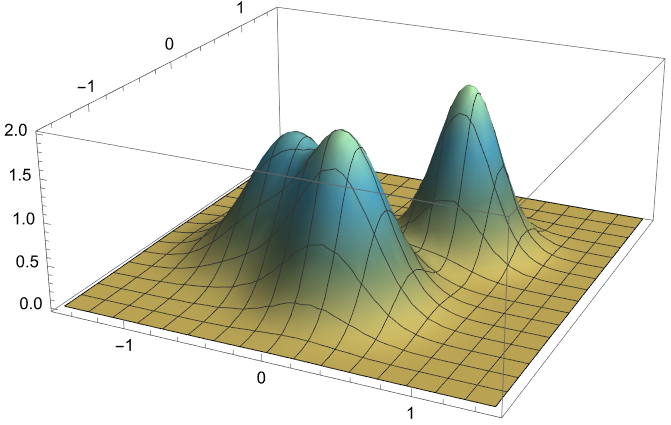
ColorFunction -> Function[{x, y, z}, jiangshanColor[1 - z]], 
PlotRange -> All]

“本质”有了，还缺一些细节。

起伏

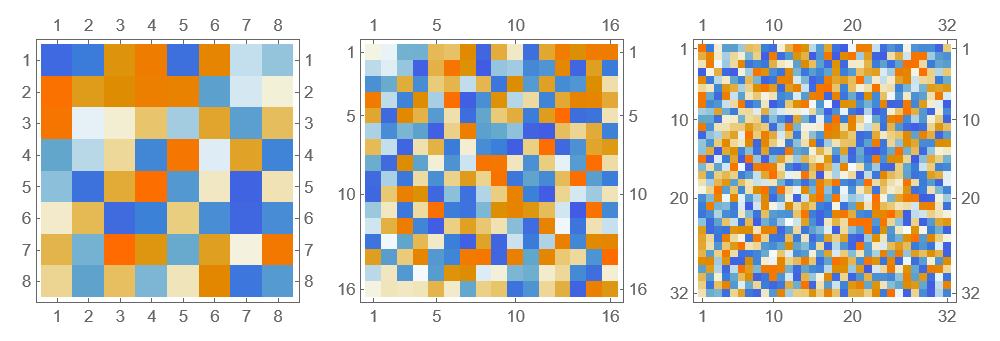
对于缺少的细节，Gemini 的建议是引入“噪声”（或说“随机纹理”）以增加山体自然感和层次感。

先生成不同粗细纹理的随机矩阵（如图），再对随机矩阵进行插值，变成二元函数。

1	MatrixPlot@Table[RandomReal[{-1, 1}], {#}, {#}] & /@ {8, 16, 32}

写成函数形式：

generateNoiseFunction[size_] := ListInterpolation[
  Table[RandomReal[{-1, 1}], {size}, {size}], {{-1.5, 1.5}, {-1.5, 1.5}}];

noise1 = generateNoiseFunction[8];
noise2 = generateNoiseFunction[16];
noise3 = generateNoiseFunction[32];

fractalNoise[x_, y_] :=
  0.5 * noise1[x, y] + (* 低频成分 *)
  0.25 * noise2[x, y] + (* 中频成分 *)
  0.125 * noise3[x, y]; (* 高频成分 *)

同样，对这部分山体起伏做一个可视化：

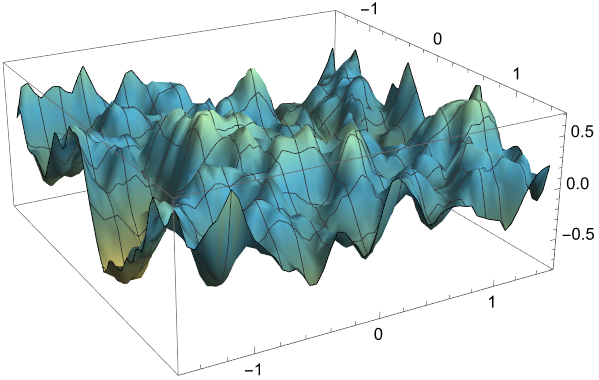
1 2	Plot3D[fractalNoise[x, y], {x, -1.5, 1.5}, {y, -1.5, 1.5}, ColorFunction -> Function[{x, y, z}, jiangshanColor[1 - z]]]

作画

结合基础山峰结构与随机纹理，就可以得到完整山形了：

1	mountainShape[x_, y_] := mainPeak[x, y] + .4 fractalNoise[x, y]

可视化语句其实很简单，就是 Plot3D[mountainShape[x, y], {x, -1.5, 1.5}, {y, -1.5, 1.5}]，只不过还加了一些不太必要的效果，能看出些阴影来。

Plot3D[
  mountainShape[x, y],
  {x, -1.5, 1.5}, {y, -1.5, 1.5},
  PlotRange -> All,
  ColorFunction -> Function[{x, y, z}, jiangshanColor[1 - z]],
  ColorFunctionScaling -> True,
  Mesh -> None,
  Axes -> False,
  Boxed -> False,
  PlotPoints -> 150,
  ImageSize -> Large,
  Lighting -> {{"Ambient", GrayLevel[0.3]}, {"Directional", White, ImageScaled[{2, 1, 2}]}}
]

目前的效果仍旧有点凑合，但我们还可以继续“求真”。

求真

印象中 Wolfram 语言是可以导入一些地理数据的，所以参考了一下 GeoElevationData 的帮助文档，其中有个例子是获取距珠穆朗玛峰半径几公里范围内的一组海拔数据：

1 2	data = GeoElevationData[Entity["Mountain", "MountEverest"], GeoRange -> Quantity[10, "Kilometers"], GeoProjection -> Automatic]

我这里获取的是十公里范围，用上前面的 ColorFunction 就算“山有山样”了：

1
2
3

ListPlot3D[Reverse[data], ImageSize -> Medium, 
ColorFunction -> Function[{x, y, z}, jiangshanColor[1 - z]], 
PlotTheme -> "Minimal", Boxed -> False, Axes -> False]

“零基础「千里江山图」入门”只是玩笑话，本文实际上是“零基础「Wolfram 语言可视化」入门”。Wolfram 语言本来就很简单，现在用 AI 来帮忙算是简单到过分了。

总之，你来提供想法，AI 是最好的帮手，“帮助文档”是最好的教练。有人说是“最好的老师”，但对我来说，传统的“老师”角色已经退场了。

25/07/12

补充

很多山峰的数据在 Wolfram 中并不是“地理实体”（比如前面的 Entity["Mountain", "MountEverest"]），更通用的方法是通过经纬度获取地理数据。

我们可以将上述代码包装成一个函数 CreateSimpleTerrainPlot：

jiangshanColor = Blend[{ 
	RGBColor[0.7, 0.6, 0.3], (* 赭石色 - 低海拔 *) 
	RGBColor[0.2, 0.5, 0.4], (* 石绿色 - 中海拔 *) 
	RGBColor[0.25, 0.5, 0.65] (* 石青色 - 高海拔 *) 
	}, #1] &;

CreateSimpleTerrainPlot[latitude_?NumericQ, longitude_?NumericQ] :=
 Module[{location, area, elevationData, plot},
  (* 1. 定义坐标和区域 *)
  location = GeoPosition[{latitude, longitude}];
  area = GeoDisk[location, Quantity[10, "Kilometers"]];
  
  (* 2. 获取海拔数据 *)
  Print["正在下载海拔数据..."];
  elevationData = GeoElevationData[area];
  Print["数据下载完成。"];
  
  (* 3. 生成图像 *)
  plot = ListPlot3D[QuantityMagnitude[elevationData],
    ImageSize -> Large, 
    ColorFunction -> Function[{x, y, z}, jiangshanColor[z]],
    PlotTheme -> "Minimal", 
    Boxed -> False, 
    Axes -> False, 
    PlotRange -> All];
    
  (* 返回生成的图像 *)
  plot]

有了这个函数，我们就可以轻松地生成不同地点的山脉图像了。比如，获取黄山莲花峰（北纬 30.12 度，东经 118.17 度）的地形：

1	CreateSimpleTerrainPlot[30.12, 118.17]

因为是“千里江山图”，再试试庐山南部某点（北纬 29.45 度，东经 116.0 度）的地形：

1	CreateSimpleTerrainPlot[29.45, 116.0]

25/07/20

Joffoo's blog

零基础「千里江山图」入门

取色

山形

起伏

作画

求真

补充

文章目录